In the exponential expression \(a^n\), the number \(a\) is called the base, while the number \(n\) is called the exponent.
Let \(a\) be any real number and let \(n\) be any whole number. If \(n \neq 0\), then: \[a^
For example, raising a number to the fifth power requires that we repeat the number as a factor five times (see Figure \(\PageIndex<1>\)). \[\begin(-2)^ &=(-2)(-2)(-2)(-2)(-2) \\[4pt] &=-32 \end \nonumber \]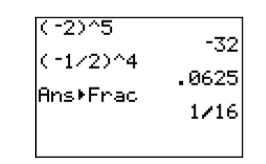 
Raising a number to the fourth power requires that we repeat that number as a factor four times. \[\begin\left(-\dfrac<1>\right)^ &=\left(-\dfrac<1>\right)\left(-\dfrac<1>\right)\left(-\dfrac<1>\right)\left(-\dfrac<1>\right) \\ &=\dfrac<1> \end \nonumber \] Remember that if there is a negative in front of the term without parentheses that the negative is not raised to the power. \[\begin-2^4 &=-1 \cdot 2^4 \\&= -1 \cdot (2)(2)(2)(2) \\&= -16 \end \nonumber \] As a final example, note that \(10^0 = 1\), but \(0^0\) is undefined (see Figure \(\PageIndex\)).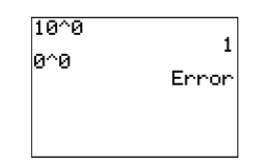 
For those who may be wondering why \(a^0 = 1\), provided \(a \neq 0\) , here is a nice argument. First, note that \(a^1 = a\), so: \[a \cdot a^<0>=a^ \cdot a^ <0>\nonumber \] On the right, repeat the base and add the exponents. \[a \cdot a^<0>=a^ \nonumber \] Or equivalently: \[a \cdot a^<0>=a \nonumber \] Now, divide both sides by \(a\), which is permissible if \(a \neq 0\) . \[\dfrac>=\dfrac \nonumber \] Simplify both sides: \[a^0 =1 \nonumber \]
In the expression \(a^n\), the number \(a\) is called the base and the number \(n\) is called the exponent. Frequently, we’ll be required to multiply two exponential expressions with like bases, such as \(x^ \cdot x^\). Recall that the exponent tells us how many times to write each base as a factor, so we can write: \[\begin x^ \cdot x^ &=(x \cdot x \cdot x) \cdot(x \cdot x \cdot x \cdot x) \\ &=x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \\ &=x^ \end \nonumber \] Note that we are simply counting the number of times that \(x\) occurs as a factor. First, we have three \(x’s\), then four \(x’s\), for a total of seven \(x’s\). However a little thought tells us that it is much quicker to simply add the exponents to reveal the total number of times \(x\) occurs as a factor. \[\begin x^ \cdot x^ &=x^ \\ &=x^ \end \nonumber \] The preceding discussion is an example of the following general property of exponents.
To multiply two exponential expressions with like bases, repeat the base and add the exponents. \[a^
Solution
In each example we have like bases. Thus, the approach will be the same for each example: repeat the base and add the exponents.
With a little practice, each of the examples can be simplified mentally. Repeat the base and add the exponents in your head: \(y^ \cdot y^=y^, 2^ \cdot 2^=2^\) and \((x+y)^(x+y)^=(x+y)^\).
Answer
Simplify: \(\left(a^ b^\right)\left(a^ b^\right)\)
Solution
We’ll use the commutative and associative properties to change the order of operation, then repeat the common bases and add the exponents.
With practice, we realize that if all of the operators are multiplication, then we can multiply in the order we prefer, repeating the common bases and adding the exponents mentally: \(\left(a^ b^\right)\left(a^ b^\right)=a^ b^\).
Answer
